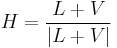Blinn–Phong shading model
The Blinn–Phong shading model (also called Blinn–Phong reflection model or modified Phong reflection model) is a modification to the Phong reflection model developed by Jim Blinn.[1]
Blinn–Phong is the default shading model used in OpenGL and Direct3D's fixed-function pipeline (before Direct3D 10 and OpenGL 3.1), and is carried out on each vertex as it passes down the graphics pipeline; pixel values between vertices are interpolated by Gouraud shading by default, rather than the more computationally-expensive Phong shading.
Contents |
Description
In Phong shading, one must continually recalculate the angle 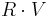 between a viewer (V) and the beam from a light-source (L) reflected (R) on a surface.
between a viewer (V) and the beam from a light-source (L) reflected (R) on a surface.
If, instead, one calculates a halfway vector between the viewer and light-source vectors,
we can replace 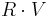 with
with  , where N is the normalized surface normal. In the above equation, L and V are both normalized vectors.
, where N is the normalized surface normal. In the above equation, L and V are both normalized vectors.
This dot product represents the cosine of an angle that is half of the angle represented by Phong's dot product if V, L, N and R all lie in the same plane. This relation between the angles remains approximately true when the vectors don't lie in the same plane, especially when the angles are small. The angle between N and H is therefore sometimes called the halfway angle.
The halfway angle is smaller than the angle desired in Phong's model, but considering that Phong is using 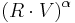 , an exponent can be set
, an exponent can be set 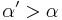 such that
such that 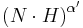 is closer to the former expression. The size of the specular highlights can be matched in this way very closely to a corresponding Phong reflection, but they will always retain a subtly different shape.
is closer to the former expression. The size of the specular highlights can be matched in this way very closely to a corresponding Phong reflection, but they will always retain a subtly different shape.
Additionally, while it can be seen as an approximation to the Phong model, it produces more accurate models of empirically determined bidirectional reflectance distribution functions than Phong for many types of surfaces. (See: Experimental Validation of Analytical BRDF Models, Siggraph 2004)
Efficiency
This rendering model is less efficient than pure Phong shading in most cases, since it contains a square root calculation. While the original Phong model only needs a simple vector reflection, this modified form takes more into consideration. However, as many CPUs and GPUs contain single and double precision square root functions (as standard features) and other instructions that can be used to speed up rendering, the time penalty for this kind of shader will not be noticed in most implementations.
However, Blinn-Phong will be faster in the case where the viewer and light are treated to be at infinity. This is the case for directional lights. In this case, the half-angle vector is independent of position and surface curvature. It can be computed once for each light and then used for the entire frame, or indeed while light and viewpoint remain in the same relative position. The same is not true with Phong's original reflected light vector which depends on the surface curvature and must be recalculated for each pixel of the image (or for each vertex of the model in the case of vertex lighting).
In most cases where lights are not treated to be at infinity, for instance when using point lights, the original Phong model will be faster.
Code sample
This sample in High Level Shader Language is a method of determining the diffuse and specular light from a point light. The light structure, position in space of the surface, view direction vector and the normal of the surface are passed through. A Lighting structure is returned;
struct Lighting
{
float3 Diffuse;
float3 Specular;
};
struct PointLight
{
float3 position;
float3 diffuseColor;
float diffusePower;
float3 specularColor;
float specularPower;
};
Lighting GetPointLight(PointLight light, float3 pos3D, float3 viewDir, float3 normal)
{
Lighting OUT;
if(light.diffusePower > 0)
{
float3 lightDir = light.position - pos3D; // FIND THE VECTOR BETWEEN THE 3D POSITION IN SPACE OF THE SURFACE
float distance = length(lightDir); // GET THE DISTANCE OF THIS VECTOR
distance = distance * distance; // USES INVERSE SQUARE FOR DISTANCE ATTENUATION
lightDir = normalize(lightDir); // NORMALIZE THE VECTOR
// INTENSITY OF THE DIFFUSE LIGHT
// SATURATE TO KEEP WITHIN THE 0-1 RANGE
// DOT PRODUCT OF THE LIGHT DIRECTION VECTOR AND THE SURFACE NORMAL
float i = saturate(dot(lightDir, normal));
OUT.Diffuse = i * light.diffuseColor * light.diffusePower / distance; // CALCULATE THE DIFFUSE LIGHT FACTORING IN LIGHT COLOUR, POWER AND THE ATTENUATION
//CALCULATE THE HALF VECTOR BETWEEN THE LIGHT VECTOR AND THE VIEW VECTOR. THIS IS CHEAPER THAN CALCULATING THE ACTUAL REFLECTIVE VECTOR
float3 h = normalize(lightDir + viewDir);
// INTENSITY OF THE SPECULAR LIGHT
// DOT PRODUCT OF NORMAL VECTOR AND THE HALF VECTOR TO THE POWER OF THE SPECULAR HARDNESS
i = pow(saturate(dot(normal, h)), specularHardness);
OUT.Specular = i * light.specularColor * light.specularPower / distance; // CALCULATE THE SPECULAR LIGHT FACTORING IN LIGHT SPECULAR COLOUR, POWER AND THE ATTENUATION
}
return OUT;
}
See also
- List of common shading algorithms
- Phong reflection model for Phong's corresponding model
- Specular highlight
References
- ^ James F. Blinn (1977). "Models of light reflection for computer synthesized pictures". Proc. 4th annual conference on computer graphics and interactive techniques: 192. doi:10.1145/563858.563893. http://portal.acm.org/citation.cfm?doid=563858.563893.